RECONSTITUTION DES CALCULS DE HELMHOLTZ
Pourquoi une telle "reconstitution" ? En 1986, j'ai publié une étude
intitulée "Valeur actuelle de l'acoustique musicale de Helmholtz", dans
laquelle je relevais un grand nombre d'erreurs risquant de mettre en
péril la théorie du savant allemand (étude disponible ici-même).
Or je ne connaissais pas, à l'époque, la principale erreur qu'il avait
faite : celle de concevoir la membrane basilaire (où s'attachent les
terminaisons du nerf auditif) comme une succession de cordes tendues
transversalement, un peu à la manière de celles d'un piano. Ainsi chaque
corde était-elle censée résonner "par influence" de manière privilégiée
à la même fréquence que le son excitateur, et l'oreille se comporter
par là comme un analyseur de fréquence. Mais la membrane basilaire est
en fait molle et se plie simplement aux mouvements du liquide dans
lequel elle baigne (voir le préambule que je donne à l'article déjà
mentionné). C'est ce que j'appelle, pour aller vite, l'erreur fondamentale
de Helmholtz. Il convient de souligner que c'est justement mon
ignorance de cette erreur, qui m'a donné l'envie d'en chercher
d'autres... et j'en ai trouvé plusieurs, ainsi que je l'explique dans
l'article de 1986. On pouvait alors se demander comment Helmholtz avait
pu atteindre le but qu'il s'était fixé. Les deux tentatives d'
"actualisation" de la théorie de Helmholtz que j'ai faites (celle de
1986 et, plus récemment, celle que j'ai publié dans le livre Du
son à la musique,
2011) ont montré qu'il fallait abandonner tout espoir d'une preuve
directement physico-physiologique du phénomène de la consonance et de
la dissonance, et qu'on était obligé d'introduire la psychologie
expérimentale dans la question. Cependant, du point de vue de
l'histoire des sciences, il est important de savoir comment Helmholtz a
opéré, comment, si l'on peut dire, il a triché
afin de plier les résultats de ses calculs à ce qu'il pensait percevoir
dans le son musical. Et pour cela, il faut d'abord reconstituer aussi
précisément que possible les calculs qu'il a effectués… qui ne sont pas
très simples et dont il ne donne pas tout le détail nécessaire. C'est
ce qu'essaie de faire la présente page.
Il s'agit de retrouver, par des moyens actuels de calcul, les résultats
de Helmholtz pour la dissonance de deux sons "en dents de scie", dont
la fréquence du premier est constante (264 Hz, soit ut2) et celle du
second variable (de 264 à 528 Hz - et même le double 1056 Hz -, soit de
ut2 à ut3 - et même ut4). Rappelons que ces résultats sont résumés et
illustrés par la figure 52A (52B pour la seconde octave, voir à la fin
de cette feuille) ayant l'allure
suivante :
1. Energie des battements d'une fibre
de la membrane basilaire
Soient
deux sons de pulsation n1 et n2 (en notation moderne on emploierait la
lettre grecque omega au lieu de n). Ils produisent, par le phénomène de
la vibration par influence, des vibrations avec battements en chaque
fibre de la membrane basilaire. Helmholtz se restreint à ne prendre que
celle où l'énergie des battements est maximale et calcule qu'elle vaut
(formule 7b page 527) :
| > |
Eb:=4*B1*B2*beta^2/(beta^2+4*pi^2*delta^2); |
 |
(1) |
B1
et B2 représent les vitesses maximales des deux vibrations (p. 526),
beta est "une quantité que nous pouvons considérer comme indépendante
de n". Nous allons voir dans un instant qu'on peut la prendre
constante; pour simplifier, nous poserons A = le carré de beta. Delta,
enfin, vaut (n1 -n2) / (n1 + n2) ; cela résulte des trois formules
données p. 527 : n1 + n2 = 2N, n1 = N(1+delta), n2 = N(1-delta).
La formule étant homogène en n1 et n2, on peut employer à leur place
les fréquences f1 et f2, plus explicites. Je prends donc, pour
l'instant avec B1 = B2 = 1 :
| > |
Eb:=A/(A+(2*pi*(f1-f2)/(f1+f2))^2); |
 |
(2) |
Tous
les calculs de Helmholtz étant faits pour f1 constante = 264 Hz
(fréquence de ut2), je restreins cette fonction à f1 = 264. En outre,
pour la viabilité des calculs Maple, j'utilise 3,14 au lieu de pi.
| > |
Eb:=(A,f2)->A/(A+(2*3.14*(264-f2)/(264+f2))^2); |
 |
(3) |
Comme
Helmholtz ne dit rien du paramètre beta (ici A), il est d'abord utile
de voir comment cette fonction évolue compte tenu du paramètre A.
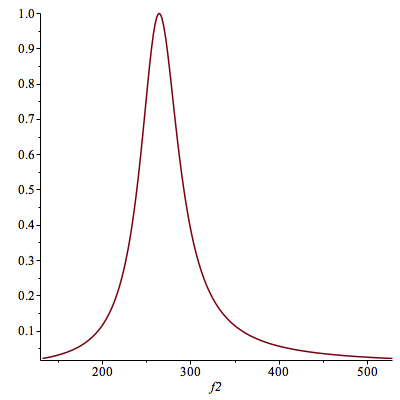
Pour A = 10 :
| > |
plot(Eb(10,f2),f2=132..528); |
Pour A = 0,1 :
| > |
plot(Eb(0.1,f2),f2=132..528); |
On constate que les petites valeurs de
A accentuent la sélectivité de la vibration par influence. A retenir
pour la suite!
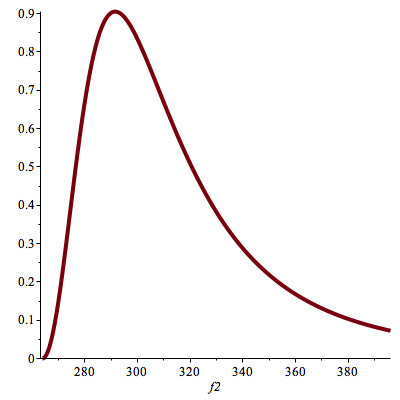
Il est d'ailleurs utile de tracer un
extrait de cette courbe entre les fréquences 264 (ut2) et 396
(sol2) :
| > |
plot(Eb(0.1,f2),f2=264..396,thickness=4); |
Cette
fonction, multipliée par la dureté propre que je vais bientôt calculer,
donnera une courbe de dissonance que l'on pourra directement comparer
avec celle qu'a tracée Helmholtz (voir ci-dessous).
On
peut encore s'amuser à tracer les variations à deux dimensions de
l'énergie des battements Eb en fonction de A et de f2 :
| > |
plot3d(Eb(A,f2),A=0.1..100,f2=132..528,axes=frame); |
2. Dureté propre
Par
ailleurs, la dissonance ressentie par l'oreille dépend non seulement de
l'énergie des battements, mais aussi de la fréquence de ces battements.
Helmholtz admet qu'à énergie égale, la dissonance est nulle pour une
fréquence nulle ou très grande, et qu'elle est maximale pour environ 30
Hz. Il choisit, à un facteur près, la fonction [60 x /(900 +
x.x)]^2, x représentant l'écart en fréquence des deux sons battant.
"C'est l'expression la plus simple qui remplisse les conditions
données, écrit-il, mais elle est naturellement arbitraire jusqu'à un
certain point."
| > |
dur:=x->(60*x/(900+x*x))^2; |
 |
(4) |
Comme
je veux faire une comparaison avec le graphique de Helmholtz et, pour
commencer, avec la courbe de dissonance du fondamental à 264 Hz avec le
fondamental à la fréquence variable f2, il faut prendre cette fonction
sur la variable x = f2 - 264, qui représente l'écart en fréquence de f2
avec f1 = 264. Donc :
| > |
dh:=f2->(60*(f2-264)/(900+(f2-264)^2))^2; |
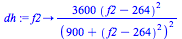 |
(5) |
| > |
plot(dh,264..396,thickness=4); |
3. Dissonance des deux fondamentaux
264 Hz et f2
Cette
dissonance est le produit de l'énergie des battements par la dureté
propre. Le résultat dépend de la constante A. Faisons donc cette
dissonance une fonction de A (et de f2) :
| > |
dissonance:=(A,f2)->A/(A+(2*3.14*(264-f2)/(264+f2))^2)*(60*(f2-264)/(900+(f2-264)^2))^2;#
Il faut expliciter les fonctions Eb et dh, sinon Maple refuse. |
 |
(6) |
| > |
plot(dissonance(1,f2),f2=264..396,thickness=4); |
Avec
cette valeur de A la dissonance reste assez élevée (environ 0,1) à 396
Hz (la quinte de 264) . Prenons un A plus petit, soit 0,1 :
| > |
plot(dissonance(0.1,f2),f2=264..396,thickness=4); |
Bon
résultat cette fois, en ce sens qu'il correspond bien à celui de
Helmholtz : par juxtaposition, nous constatons qu'il s'identifie à
la courbe notée "1:1", celle qui correspond à la contribution des
fondamentaux dans la dissonance des deux sons en dents de scie. C'est
le résultat que j'annonçais ci-dessus (avant la fin du paragraphe 1).
Courbe "1:1" de Helmholtz, extraite de la figure 52A p. 247 :
4. Reconstitution de la dissonance des
deux sons en dents de scie
Il
suffit à présent de sommer, comme l'avait fait Helmholtz, les
contributions à la dissonance de tous les couples de partiel de chacun
des deux sons : les 10 premiers partiels du ut2 (264 Hz) avec les
10 premiers du son de fréquence f2 (s'étendant de ut2 à ut3, 264 à 528
Hz). On se limite au 10 premiers partiels, comme Helmholtz.
Il
faut donc maintenant faire intervenir le produit des vitesses B1 et B2,
mentionné au début. D'après la décomposition en série de Fourier de la
fonction dents de scie, ce produit est proportionnel à 1/(m1.m2), où m1
et m2 sont les ordres des partiels des sons 1 et 2. C'est ce qu'écrit
Helmholtz p. 527 (avec un coefficient a2 qu'on peut considérer comme
constant).
Ici
les fonctions Eb et dh doivent être plus générales que ci-dessus, les
fréquences concernées étant m1.f1 et m2.f2, celles de chaque partiel.
Commençons par l'énergie de
battements. La fonction précédente doit être divisée par m1.m2 :
| > |
Eb:=(A,m1,m2,f2)->1/(m1*m2)*A/(A+(2*3.14*(m1*264-m2*f2)/(m1*264+m2*f2))^2); |
 |
(7) |
Poursuivons par la dureté propre,
maintenant pour les fréquences m1.f1 et m2.f2 :
| > |
dh:=(m1,m2,f2)->(60*(m2*f2-m1*264)/(900+(m2*f2-m1*264)^2))^2; |
 |
(8) |
La dissonance est le produit de ces
deux fonctions :
| > |
diss:=(A,m1,m2,f2)->1/(m1*m2)*A/(A+(2*3.14*(m1*264-m2*f2)/(m1*264+m2*f2))^2)*(60*(m2*f2-m1*264)/(900+(m2*f2-m1*264)^2))^2; |
 |
(9) |
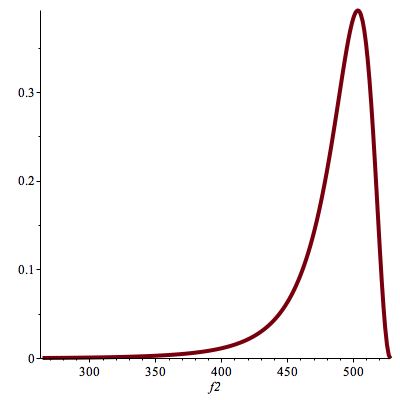
Un exemple. A = 0,1, m1 = 2, m2 = 1,
f2 de 264 à 528 :
| > |
plot(diss(0.1,2,1,f2),f2=264..528,thickness=4); |
Un autre exemple. A = 0,1, m1 = 1, m2
= 1, f2 de 264 à 528 :
| > |
plot(diss(0.1,1,1,f2),f2=264..528,thickness=4); |
Notons
en passant que ces deux exemples correspondent respectivement aux
courbes "1:2" et "1:1" dans la figure 52A de Helmholtz. Puisque, dans
l'expression de la dissonance, l'énergie des battements est divisée par
les vitesses m1 et m2, il n'est pas surprenant que le maximum de la
courbe "1:2" est inférieur à celui de la courbe "1:1". Or sur la figure
52A c'est le contraire (voir ci-dessus, au début). Il s'agit d'une
erreur de Helmholtz... que j'ai mis presque trente ans à débusquer!
Pour tracer la courbe générale, je
pose f2 = k.f1, soit f2 = 264.k, la variable k allant de 1 à 2.
| > |
dissh:=(A,m1,m2,k)->1/(m1*m2)*A/(A+(2*3.14*(m1-m2*k)/(m1+m2*k))^2)*(60*(m2*264*k-m1*264)/(900+(m2*264*k-m1*264)^2))^2; |
 |
(10) |
| > |
dissonanceh:=A->add(add(dissh(A,m1,m2,k),m1=1..10),m2=1..10); |
 |
(11) |
| > |
plot(dissonanceh(0.1),k=1..2,color=black); |
On
note que le coefficient A doit être petit pour retrouver une courbe
semblable à celle de Helmholtz. Avec A = 1, il reste une dissonance non
négligeable à la quinte :
| > |
plot(dissonanceh(1),k=1..2,color=blue); |
On peut encore s'amuser à tracer la
surface représentant la dissonance en fonction de A variable :
| > |
plot3d(dissonanceh(A,k),A=0.1..10,k=1..2,axes=frame); |
Pour visionner cette surface en mouvement
(à défaut, pour l'instant, de pouvoir la manipuler avec la souris)
aller ici.
On peut enfin tracer la courbe de
dissonance sur la deuxième octave, comme le fait Helmholtz (figure 52B
de la page 247).
| > |
plot(dissonanceh(0.1),k=2..4,color=black); |
Cette
fois, la courbe ne correspond pas bien à celle de Helmholtz (dans
laquelle la dissonance autour de la quinte est beaucoup plus forte). On
peut toutefois améliorer la correspondance en diminuant le facteur
A :
| > |
plot(dissonanceh(0.01),k=2..4,color=black); |
Rappel
de la figure 52B p. 427 pour
la dissonance sur la seconde octave :
On pourra poursuivre la lecture par la feuille d'actualisation de la
théorie de Helmholtz grâce à la psychophysiologie.
Patrice Bailhache,
28/11/2014