THÉORIE PSYCHOPHYSIOLOGIQUE DES CONSONANCES ET DISSONANCES 

Cette feuille présente, sous une forme améliorée et simplifiée, les calculs que j'ai proposés pour "actualiser" la théorie de l'acoustique musicale de Helmholtz. On trouvera un exposé détaillé de la démarche dans le livre Du son à la musique. Le principe général est d'abandonner toute étude mécanique de l'oreille interne, en conservant tout de même l'idée que la dissonance provient des battements qui se produisent dans la cochlée et que l'audition additionne les dissonances selon les règles acoustiques de la psychologie expérimentale. 

Bien que son contenu soit indépendant de celui de la feuille de reconstitution des calculs de Helmholtz, il serait préférable que cette dernière soit lue préalablement à la présente.

1. Bande critique et dissonance élémentaire 

Ces fonctions sont établies expérimentalement et valent pour un individu "moyen"; autrement dit, elles résultent d'analyses statistiques sur un grand nombre de personnes. 

1.1. Calcul de la bande critique bc en fonction de la fréquence moyenne f = (f1+f2)/2 de deux sons simples de fréquences f1 et f2. 

Lorsque deux sons simples produisent des battements, ceux-ci sont perçus comme dissonants seulement lorsque la différence des fréquences des sons est inférieure à une certaine valeur, appelée bande critique, elle-même fonction de la fréquence moyenne des sons. A l'intérieur de cette bande critique, la dissonance est une fonction "en cloche" de la différence des fréquences : elle commence par croitre à partir de zéro, passe par un maximum et décroit jusqu'à zéro lorsque la différence excède la bande critique. 

>

restart;

 

>	bc:=f->0.2022*(1408969+f^2)^.5-150;# (Ne pas mettre la fonction sqrt au lieu de ^.5. Maple refuse de calculer.)

 

Graphique de la fonction bande critique, bc, en fonction de la différence des fréquences des deux sons simples : 

>	plot(bc,20..4000,thickness=4,color=black);

 

1.2. Calcul de la dissonance élémentaire de de deux sons simples de fréquences f1 et f2 

1.2.1. Première étape : comme la fonction |f2 - f1|/bc intervient deux fois, je commence par calculer la fonction dnf (pour "différence normalisée des fréquences"), qui varie de 0 à 1 lorsque la différence des fréquences augmente de 0 jusqu'à la valeur de la bande critique. 

>	dnf:=(f1,f2)->abs(f2-f1)/bc((f1+f2)/2);# Je prends la moyenne arithmétique... pas gênant.

 

1.2.2. Deuxième étape : calcul proprement dit de la dissonance élémentaire. Cette dissonance est la valeur de la fonction ci-dessous lorsqu'on remplace la variable x par dnf. 

>	de:=x->118*x^2*exp(-8*x);

 

Par définition cette fonction atteint son maximum égal à 1 pour x = 0,25 (la dissonance élémentaire, valeur psychologique, n'est évidemment définie qu'à un facteur près. C'est pourquoi, pour simplifier, on a choisi une fonction dont le maximum est 1). 

Graphique de la dissonance élémentaire pour dnf dans [0,5], c'est-à-dire pour la différence des fréquences variant de 0 jusqu'à cinq fois l'amplitude de la bande critique. 

>	plot(de,0.. 5,thickness=4,color=black);

 

Calculons la valeur de la dissonance élémentaire lorsque la différence des fréquences égale une fois et demi la bande critique : 

>	evalf(de(1.5));

 

(1)

 

Elle ne vaut que 1,6 milième, ce qui justifie bien la signification de bande critique (dissonance quasi nulle en dehors d'elle). 

2. Intensité des battements 

Calcul de l'intensité psychologique des battements. On montre par l'expérience qu'elle est égale, en sones, à un facteur près, à l'énergie physique en W/m2 portée à la puissance 0,3. Les partiels d'ordre m1 et m2 de deux sons en dent de scie ont une énergie physique respectivement proportionnelle à 1/m1 et 1/m2 (cela résulte de la décomposition en série de Fourier de la fonction dents de scie). On a donc : 

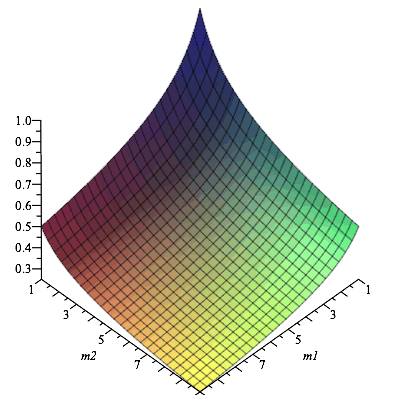
>	IBpsy:=(m1,m2)->(1/m1/m2)^0.3;

 

(2)

 

On peut tracer une surface représentant la variation de IBpsy en fonction de chacune des variables m1 et m2 : 

>	plot3d(IBpsy(m1,m2),m1=1..10,m2=1..10,axes=frame);

 

3. Dissonance de deux sons en "dents de scie" 

Il faut ajouter les dissonances élémentaires multipliées par l'intensité des battements pour chaque couple de partiel des deux sons complexes (on se limite aux 10 premiers partiels). Mais lorsque les partiels sont situés dans une même bande critique, l'intensité perçue de leur combinaison est plus faible que la somme des intensités de chacun d'eux (alors qu'elle est égale à cette somme s'ils sont en dehors de toute bande critique). Il se produit donc une sorte d'atténuation par recouvrement. Une étude détaillée(*) montre qu'il faut approximativement conserver les contributions telles quelles jusqu'au rang 4 (lorsque m1+m2<=8; pas de recouvrement de bande critique dans ce cas), les multiplier par 0,6 pour 8<m1+m2<=14 et par 0,4 pour m1+m2>14. 

(*) Cette étude détaillée est faite dans les pages 188-191 du livre cité Helmholtz, Du son à la musique. 

Pour le m1e partiel du son de fréquence fondalentale f1 = 264 (ut2), le m2e partiel du son de fréquence fondamentale f2 = 264.k (k de 1 à 2, donc f2 de 264 à 528, i.e. de ut2 à ut3): 

>	diss:=(m1,m2,k)-> if m1+m2<=8 then IBpsy(m1,m2)*de(dnf(264*m1,264*k*m2)) elif m1+m2<=14 then 0.6*IBpsy(m1,m2)*de(dnf(264*m1,264*k*m2)) else 0.4*IBpsy(m1,m2)*de(dnf(264*m1,264*k*m2)) fi;

 

(3)

 

A fin de comparaison, je calcule la même dissonance, mais sans aucune atténuation des contributions se recouvrant dans des bandes critiques: 

>	dissbrute:=(m1,m2,k)->IBpsy(m1,m2)*de(dnf(264*m1,264*k*m2));

 

(4)

 

La dissonance des deux sons complexes est la somme des dissonances des 10x10 =100 couples de partiels : 

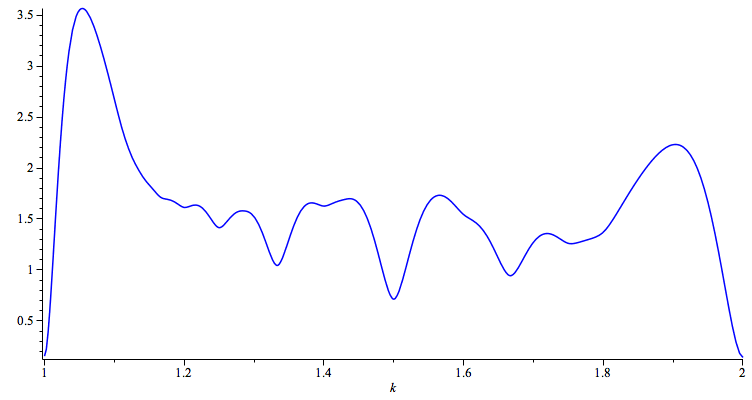
>	dissonance:=add(add(diss(m1,m2,k),m1=1..10),m2=1..10):

 

Faisant varier k de 1 à 2, c'est-à-dire f2 de f1 = 264 à 2.f2 = 528, j'obtiens le graphique : 

>	plot(dissonance,k=1..2,color=blue);

 

Et pour la dissonance sans atténuation pour les partiels de fréquences élevées : 

>	dissonancebrute:=add(add(dissbrute(m1,m2,k),m1=1..10),m2=1..10):

 

>	plot(dissonancebrute,k=1..2,color=red);

 

Je peux comparer ces deux fonctions sur un même graphique  : 

>	plot([dissonance,dissonancebrute],k=1..2,color=[blue,red]);

 

On voit que l'atténuation des dissonances des contributions situées dans les bandes critiques (courbe bleue) réduit significativement la dissonance générale (courbe rouge). 

 Pour finir, il convient sans doute de rappeler ici les hypothèses sur lesquelles repose cette étude et les perspectives d'étude qu'elles suggèrent.

Comme je l'écris dans le livre mentionné au début de cette feuille, quitte à procéder par la psychologie expérimentale, on pourrait objecter qu’il serait bien plus efficace et « expéditif » d’établir une courbe de dissonance généralisée semblable à celle qui précède, par mesure directe, sans analyse ni calcul, sur un large échantillon d’individus. Mais justement, on perdrait tout alors, puisqu’il n’y aurait plus aucune analyse; et la question se poserait de nouveau, sans réponse, de savoir pourquoi il y a des minima de dissonance pour certains intervalles (l’octave, la quinte, etc.). Cela montre clairement que la démarche que j’ai suivie produit bien un résultat spécifique non négligeable.

1) Pour mener les calculs, j'ai supposé que les intensités psychologiques de battements s’ajoutent selon les mêmes lois que les intensités psychologiques des sons purs (la formule que j'ai adoptée pour l'intensité des battements est en fait celle de l'intensité des sons purs, les lois d'atténuation des additions des dissonances sont en fait celles des additions des sons). Il faudrait commencer par effectuer un ensemble de tests expérimentaux pour établir les lois concernant les intensités de battements : ce serait un travail fastidieux mais non impossible; je donne ici du pain sur la planche aux psychologues expérimentaux!
2) J'ai aussi négligé la variation de la sensibilité de l’oreille selon la fréquence, variation qui est bien connue en ce qui concerne les sons eux-mêmes (cf. les courbes d'égales intensités sonores physiologiques. La sensibilité de l'oreille est maximale vers 3500 Hz). Il faudrait examiner comment sont perçus des battements d'égale vitesse à des fréquences différentes (par exemple des battements à 30 Hz produits d'une part par les sons purs à 200 et 230 Hz, d'autre part par les sons purs à 3000 et 3030 Hz). Encore du travail pour les expérimentateurs en psychologie...
3) Comme je l'explique dans le livre Du son à la musique (pp. 189-191), la règle générale d'évaluation de l'intensité psychologique de l'addition d'un nombre quelconque de sons purs, que j'ai établie, est très difficile à mettre en oeuvre. J'ai simplifié les choses en utilisant des règles d'atténuation (voir au début du paragraphe 3 ci-dessus). Cette fois j'en appelle aux calculateurs et informaticiens. Au demeurant, pour ce troisième cas, le bénéfice serait probablement réduit, car mes hypothèses d'atténuation résument avec vraisemblance les situations possibles de mélanges de sons.

En supposant qu'on a déjà étudié la feuille de la reconstitution des calculs de Helmholtz, on pourra maintenant poursuivre la lecture par la feuille de comparaison de la théorie de Helmholtz avec la théorie actualisée.

Patrice Bailhache, 29/11/2014