COMPARAISON DES RÉSULTATS DE HELMHOLTZ
AVEC CEUX DE SON "ACTUALISATION" PSYCHOPHYSIOLOGIQUE
Dans
cette feuille de calcul je compare les résultats de Helmholtz avec ceux
de la théorie psychophysiologique que j'ai établie. Pour être comprise,
cette feuille suppose la connaissance préalable des deux
précédentes : "Reconstitution
des calculs de Helmholtz" et
"Théorie psychophysiologique des
consonnances et dissonances".
1. Dissonance élémentaire
Je
prendrai cette dissonance élémentaire pour deux sons (simples - c'est
cela que veut dire "élémentaire") de fréquence f1 = 264 Hz (ut2) et f2
variable de 264 à 396 Hz (sol2).
1.1.
Chez Helmholtz, nous avons trouvé que la dissonance est le produit de
l'énergie des battements par la dureté propre, le résultat dépendant
d'une constante A.
A
= 0,1 donnait un résultat très voisin de celui de Helmholtz, nous
avions (la fonction deh était simplement appelée "dissonance") :
| > |
deh:=(A,f2)->A/(A+(2*3.14*(264-f2)/(264+f2))^2)*(60*(f2-264)/(900+(f2-264)^2))^2; |
 |
(1) |
| > |
plot(deh(0.1,f2),f2=264..396,thickness=4,color=black); |
(Nous présentions cette courbe
applatie selon les ordonnées, afin de l'identifier à celle de la figure
52A p. 247 de la Théorie physiologique de la musique.)
1.2. Dans la théorie
psychophysiologique, la dissonance élémentaire est donnée par la
fonction :
| > |
de:=x->118*x^2*exp(-8*x); |
 |
(2) |
dans laquelle x représente la
différence normalisée des fréquences des deux sons en dissonance. On a
vu que x était :
| > |
abs(f2-f1)/bc((f1+f2)/2); |
 |
(3) |
Ici f1 = 264, f2 varie de 264 à 396 et
bc est la bande critique donnée par la fonction :
| > |
bc:=f->0.2022*(1408969+f^2)^.5-150; |
 |
(4) |
On a donc finalement :
| > |
depsy:=f2->118*(abs(f2-264)/bc((264+f2)/2))^2*exp(-8*abs(f2-264)/bc((264+f2)/2)); |
 |
(5) |
| > |
plot(depsy,264..396,thickness=4,color=blue); |
On voit que les fonctions deh et depsy
(qui ne sont définies qu'à un facteur près) ont des allures tout à fait
semblables.
2. Intensité des battements
Chez
Helmholtz l'intensité des battements multipliée par ce qu'il appelle la
dureté propre donne la dissonance élémentaire. Dans la théorie
psychophysiologique la dissonnance élémentaire tient déjà compte
implicitement de l'intensité des battements. Ainsi, pour réaliser la
comparaison des deux théories, il considérer seulement les
multiplicateurs propres aux ordres des partiels des deux sons en dents
de scie. Chez Helmholtz c'est le terme B1.B2, qui est proportionnel à
1/(m1.m2) et dans la théorie psychophysiologique c'est ce même terme à
la puissance 0,3 (ainsi le veut la loi de l'audition, voir le fichier
des calculs dans cette théorie). On peut donc très simplement comparer
ces fonctions (en les prenant à un facteur près).
2.1. Helmholtz :
| > |
plot3d(IBh(m1,m2),m1=1..10,m2=1..10,axes=frame); |
2.2. Théorie psychophysiologique :
| > |
IBpsy:=(m1,m2)->(1/m1/m2)^0.3; |
 |
(6) |
| > |
plot3d(IBpsy(m1,m2),m1=1..10,m2=1..10,axes=frame); |
Comparons les valeurs de cette
intensité lorsque d'une part m = 1 et n = 10, d'autre part m = n = 10,
dans les deux théories
| > |
evalf(IBh(1,10));evalf(IBh(10,10)); |
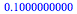 |
 |
(7) |
| > |
evalf(IBpsy(1,10));evalf(IBpsy(10,10)); |
 |
 |
(8) |
On
constate que l'hypothèse (fausse) de Helmholtz donne des valeurs bien
inférieures à celles de la théorie psychophysiologique (exactes). Cela
explique en grande partie les résultats "optimistes" de Helmholtz.
3. Dissonance de deux sons en "dents
de scie"
3.1 Helmholtz
Je reprends :
| > |
dissh:=(A,m1,m2,k)->1/(m1*m2)*A/(A+(2*3.14*(m1-m2*k)/(m1+m2*k))^2)*(60*(m2*264*k-m1*264)/(900+(m2*264*k-m1*264)^2))^2; |
 |
(9) |
| > |
dissonanceh:=A->add(add(dissh(A,m1,m2,k),m1=1..10),m2=1..10); |
 |
(10) |
| > |
plot(dissonanceh(0.1),k=1..2,color=black); |
3.2. Théorie psychophysiologique
Il faut commencer par généraliser la
fonction depsy ci-dessus à une fréquence f1 non constante égale à 264.
| > |
depsy:=(f1,f2)->118*(abs(f2-f1)/bc((f1+f2)/2))^2*exp(-8*abs(f2-f1)/bc((f1+f2)/2)); |
 |
(11) |
On prend alors pour f1 et f2 les
fréquences des partiels m1.264 et k.m2.f2 :
| > |
disspsy:=(m1,m2,k)->
if m1+m2<=8 then IBpsy(m1,m2)*depsy(264*m1,264*k*m2)
elif m1+m2<=14 then 0.6*IBpsy(m1,m2)*depsy(264*m1,264*k*m2)
else 0.4*IBpsy(m1,m2)*depsy(264*m1,264*k*m2)
fi; |
| > |
dissonancepsy:=add(add(disspsy(m1,m2,k),m1=1..10),m2=1..10): |
| > |
plot(dissonancepsy,k=1..2,color=blue); |
C'est la courbe obtenue dans la
feuille "Théorie psychophysiologique des consonances et des
dissonances".
Nous
pouvons maintenant présenter dans un même graphique la courbe de
Helmholtz et celle que nous venons d'obtenir. Il faut à cette fin
mettre les ordonnées à peu près à la même échelle.
| > |
plot([4.2*dissonanceh(0.1),dissonancepsy],k=1..2,color=[black,blue]); |
Nous
constatons que pour des maxima de dissonance égaux près de l'unisson et
de l'octave (k = 1 et 2), les dissonances de la théorie
psychophysiologique sont beaucoup plus élevées que celles de Helmholtz.
Patrice Bailhache, 28/11/2014











